before...
복잡도 (Complexity)
복잡도는 알고리즘의 성능을 나타내는 척도인데, 시간 복잡도와 공간 복잡도로 나눌 수 있다. 시간 복잡도는 속도에 해당하는 알고리즘의 수행시간 분석결과를 말한다. 공간 복잡도는 메모리 사용량에 대한 분석결과를 말한다. 쉽게 설명하면 아래와 같다.
✔️ 시간복잡도 = 얼마나 오래 걸리는가
✔️ 공간복잡도 = 얼마나 메모리를 차지하는가
빅오(Big-O) 표기법?
빅오 표기법은 알고리즘의 효율성을 평가하기 위한 분석 방법이다. 효율성의 판단 기준은 바로 위에서 설명한 시간 복잡도, 공간 복잡도이다. 보통 실행속도가 메모리 사용량보다 중요하기 때문에 성능을 판단할 때는 시간 복잡도에서 가장 영향력이 큰 부분을 따진다.
빅오 표기법은 기본적으로 '최악의 경우'를 가정하고 알고리즘의 성능을 판단한다. 이게 무슨 말인지 간단한 예제를 보면서 이해해보자.
아래 예제에서 시간 복잡도는 O(1)로 표현한다. 연산(+)이 딱 한번만 일어나기 때문이다. 참고로 여기서 말하는 '연산'은 사칙 연산, 비교 연산같은 기본적인 연산을 말한다.
let a = 1;
let b = 2;
console.log(a + b);
그럼 이런 경우는 어떨까? 여기서 시간복잡도는 O(n)이라고 표현한다. 데이터 개수를 n개라고 했을 때 n번의 연산이 일어나기 때문이다.
let arr = [1, 2, 3, 4, 5];
let sum = 0;
for (let i in arr) {
sum += i;
}
빅오 표기법 종류

✔️ O(1) : 상수 시간 (데이터 수에 상관X, 연산횟수 고정)
✔️ O(log n) : 로그 시간 (데이터 수 증가율 > 연산횟수 증가율)
✔️ O(n) : 선형 시간 (데이터 수 & 연산횟수 비례)
✔️ O(n* log n) : 로그 선형 시간 (데이터의 수 2배 증가 → 연산횟수 2배 조금 넘게 증가)
✔️ O(c^n): 지수 시간 (지수적으로 무섭게 증가..)
이 외에도 아래와 같이 다양한 빅오 표기법들이 있다. 위쪽에 있을수록 더 빠르기 때문에, 성능도 더 좋다고 판단된다. 오른쪽 그래프는 데이터 수가 늘어남에 따라 수행에 걸리는 시간을 비교한 것이다.

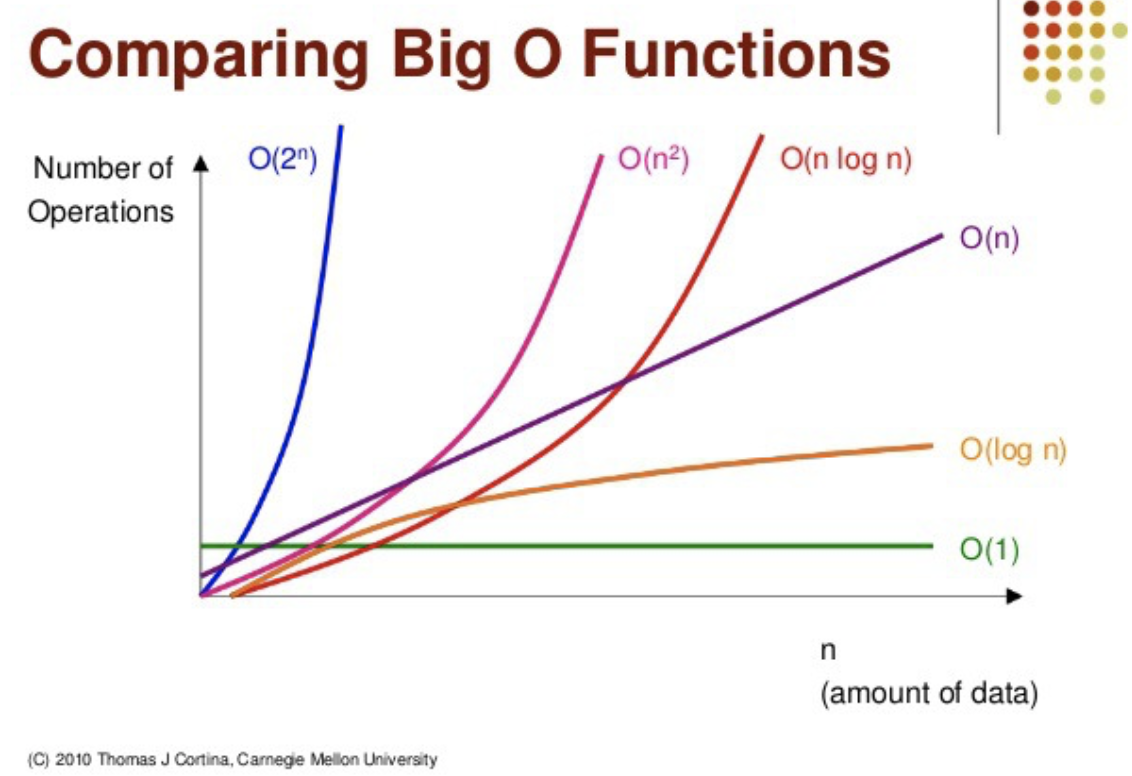
빅오 표기법의 성능
O(1) > O(log n) > O( n) > O( n* log n ) > O( n²) > O( n³) > O( 2n ) > O( n! )
자료구조 & 시간복잡도
1. Arrays (배열)
(Javascript에서의 배열이 아닌 평범한 배열구조라고 가정한다)
|
할당 (Assign) |
O(n) |
바로 접근 후 덮어쓰기 가능 |
| 삽입 (Insert) | O(n) | 하나씩 옮겨야 함 (최악의 경우 모든 요소를 옮겨야 함) |
| 삭제 (Remove) | O(1) | 삽입처럼 삭제 후 하나씩 옮겨야 함 |
| 검색 (Lookup - position) | O(1) | 특정위치 데이터 가져오기 바로 접근 가능 |
| 검색 (Find - value) | O(n) | 특정 값 찾기 하나씩 비교해서 찾아야 함 |
2. Linked Lists (연결 리스트)
|
할당 (Assign) |
O(n) |
head부터 다음으로 계속 넘어가며 비교 필요 |
| 삽입 (Insert) | O(1) | 검색 이후 → O(1) / 검색 포함 → O(n) |
| 삭제 (Remove) | head → O(1) middle → O(n) |
- |
| 검색 (Lookup - position) | O(n) | head부터 다음으로 계속 넘어가며 비교 필요 |
| 검색 (Find - value) | O(n) | head부터 다음으로 계속 넘어가며 비교 필요 |
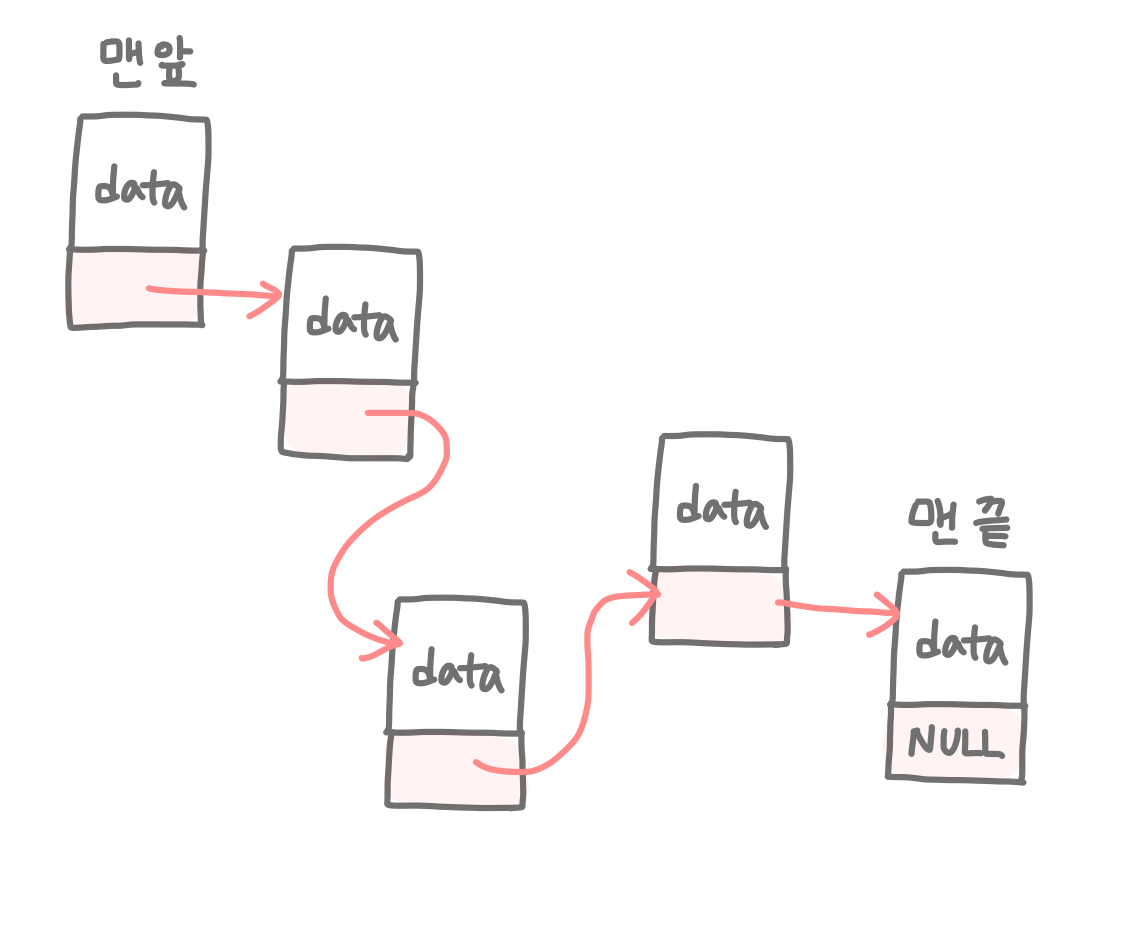
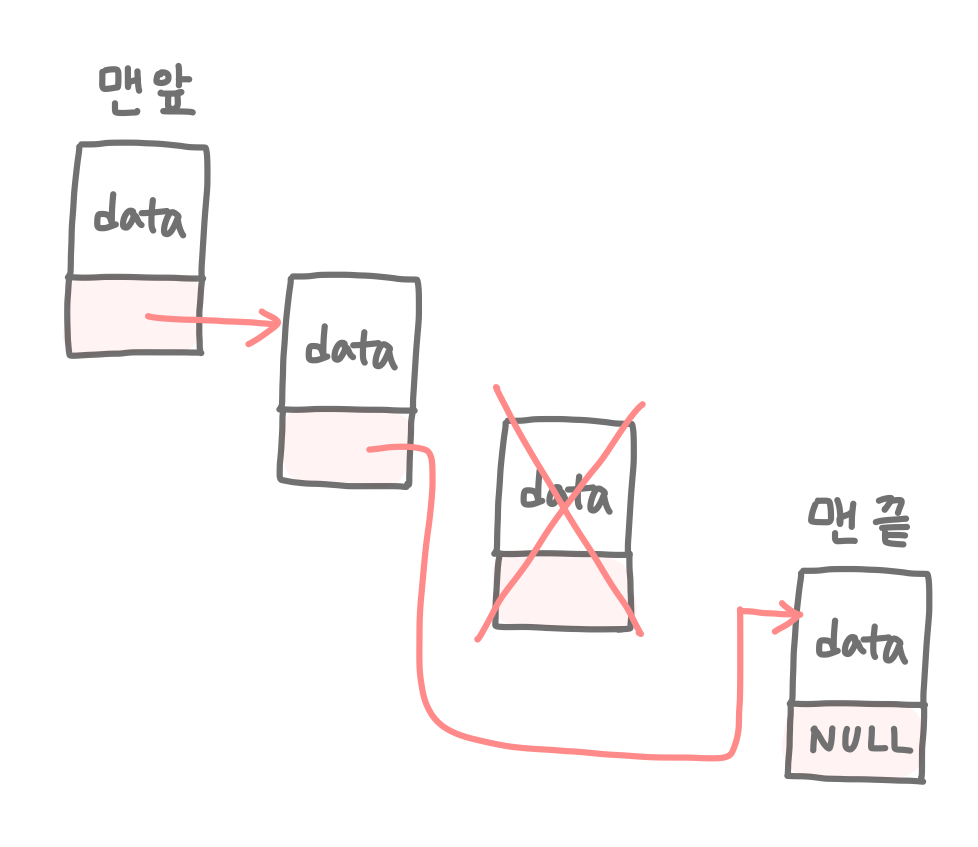
참고로, Doubly-Linked List (이중 연결 리스트)는 자신의 양쪽 노드를 모두 참조하기 때문에, 삭제 과정이 단일 연결리스트보다 빠르다. 하지만 메모리를 더 많이 차지한다는 단점이 있다.
Trede-Off
배열 : 위치찾기 O(1), 추가/삭제 O(n)
연결리스트 : 추가 O(1), 삭제/위치찾기 O(n)
이중연결리스트 : 추가/삭제 O(1), but 메모리 차지 늘어남
'Base > 알고리즘' 카테고리의 다른 글
| 퀵 정렬(Quick Sort) (0) | 2021.06.01 |
|---|---|
| DFS(깊이우선탐색) / BFS(너비우선탐색) (0) | 2021.01.24 |
| 선형 검색, 이진 검색 (단순 검색 알고리즘) (0) | 2021.01.09 |
| 꼬리 재귀 (Tail Recursion) (7) | 2021.01.08 |




댓글