재귀 자체도 머리 속에 과정을 떠올리려고 하면 굉장히 추상적이라 어렵게 느껴지는데 꼬리 재귀 개념까지 한번에 이해하려고하니 글을 읽는 것만으로는 잘 이해가 되지 않았다. 개발자 도구를 이용해 디버깅해보며 스택이 어떤 식으로 변하는 지도 살펴보고, 내 관점에서 이해한 바를 그림으로도 그려보기도 했다. 덕분에 꼬리재귀가 어떻게 스택오버플로우 문제를 개선할 수 있다는 건지 이해할 수 있었다. 하지만 아직 설명할 부분들이 좀 더 있는 것 같아 내용은 계속해서 수정, 보충할 예정이다. (잘못 알고있거나 보충할 내용이 있다면 알려주시면 감사하겠습니다🙏🏻)
재귀 (Recursion)
꼬리 재귀에 대한 이야기를 하기 전에 '재귀'가 뭔지, 그리고 일반적인 재귀의 위험성에 대해 먼저 간단히만 이야기하고 넘어가려 한다. 재귀함수란 한 마디로 '자기 자신을 호출하는 함수'이다. 구조는 비슷하지만 더 작은 문제로 쪼갤 수 있는 문제를 풀 때 유용한 접근 방법이다. 재귀를 사용하면 코드가 짧아지고 내용도 직관적으로 파악할 수 있어 가독성이 높아진다는 장점이 있다.
앞서 말했듯이 재귀를 사용하면 함수를 여러 번 호출하게 된다. 그렇다면 이 때 메모리엔 어떤 변화가 생길까? 우선 함수가 한 번씩 호출될 때마다 함수의 입력값(매개변수), 결과값(리턴값), 그리고 리턴 후 돌아갈 위치 등이 스택(Stack)이라는 데이터 저장 공간에 보관된다.
그런데 재귀는 호출의 호출의 호출의 호출의 호출ㅇ.....을 반복하기 때문에 무리하게 호출하면 이 스택이라는 공간이 다 차버리는 '스택 오버 플로우' 현상을 일으킬 수 있다. 엄청난 위험성을 가지고 있는 것이다.
✔️ 요약 : 재귀 함수는 호출 시 마다 스택 공간에 뭔가를 저장하기 때문에, 무리하게 호출하면 '스택 오버플로우'가 발생할 수 있다!
꼬리재귀 (Tail Recursion)
재귀는 물론 장점이 분명해서 자주 사용된다. 하지만 굉장히 위험(?)하기 때문에 주의해서 사용해주어야 한다. 재귀함수의 장점은 살리고, 단점은 보완하는 방법 중 하나가 바로 '꼬리 재귀'이다.
꼬리 재귀는 '재귀 호출이 끝나면 아무 일도 하지 않고 결과만 바로 반환되도록 하는' 방법이다. 이 방식을 사용하면 이전 함수의 상태를 유지하지도 않고 추가 연산을 하지도 않아서 스택이 넘쳐나는 문제를 해결할 수 있게 된다.
꼬리 재귀 함수는 이름처럼 항상 함수의 꼬리부분(마지막)에서 실행되는데, return되기 전에 값이 정해지며 호출당한 함수의 결과값이 → 호출하는 함수의 결과값으로 반환된다.
✔️ 꼬리 재귀 : 호출 당한 함수의 결과 → 호출한 함수의 결과
이렇게 글로 본다고 바로 이해가 되지 않을 것이다,, (나는 그랬다) 일단은 호출 '당한' 함수, 그리고 호출'한' 함수가 있다는 정도만 기억해두고 예제를 보면서 천천히 이해해보자.
재귀 vs 꼬리재귀
우선 재귀하면 가장 먼저 떠오르는 팩토리얼(!) 예제를 일반적인 재귀, 꼬리 재귀로 구현했을 때 어떤 차이가 있는 지 한번 비교해보자. (개발자 도구를 열어 직접 디버깅을 하며 스택이 어떤 식으로 변하는지 직접 눈으로 확인해보면 더 이해하기 쉬울 것이다)
일반 재귀 방식
function factorial(n) {
if (n === 1) {
return 1;
}
return n * factorial(n-1);
}
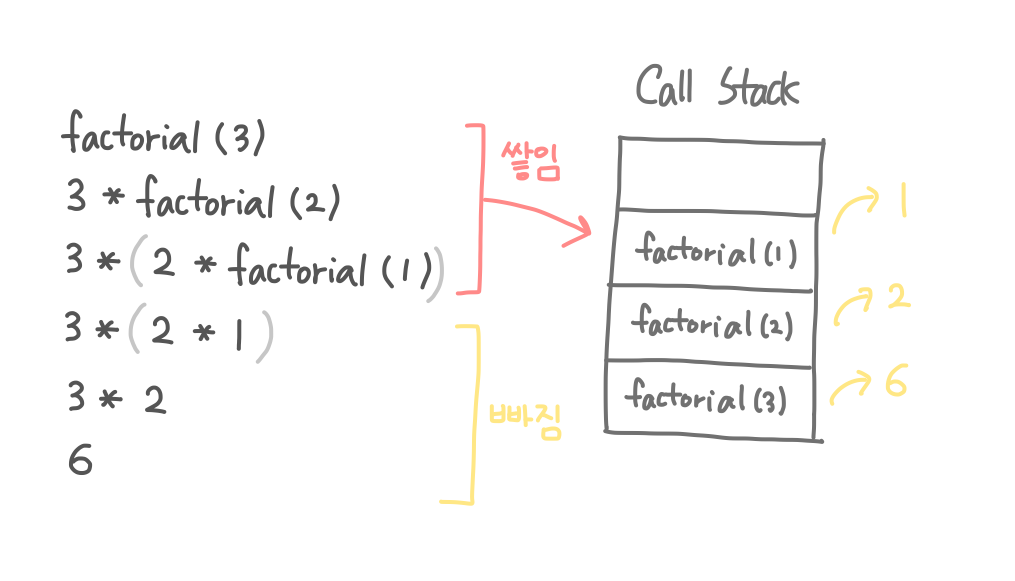
n값으로 3을 넣었을 때, 스택이 어떻게 변하는 지를 그림으로 그려보았다. 빨간색으로 표시된 부분까지는 호출당한 함수들이 쭉 스택에 쌓인다. 그리고 노란색으로 표시된 부분부터는 각자가 자신이 계산한 값들을 반환한다.
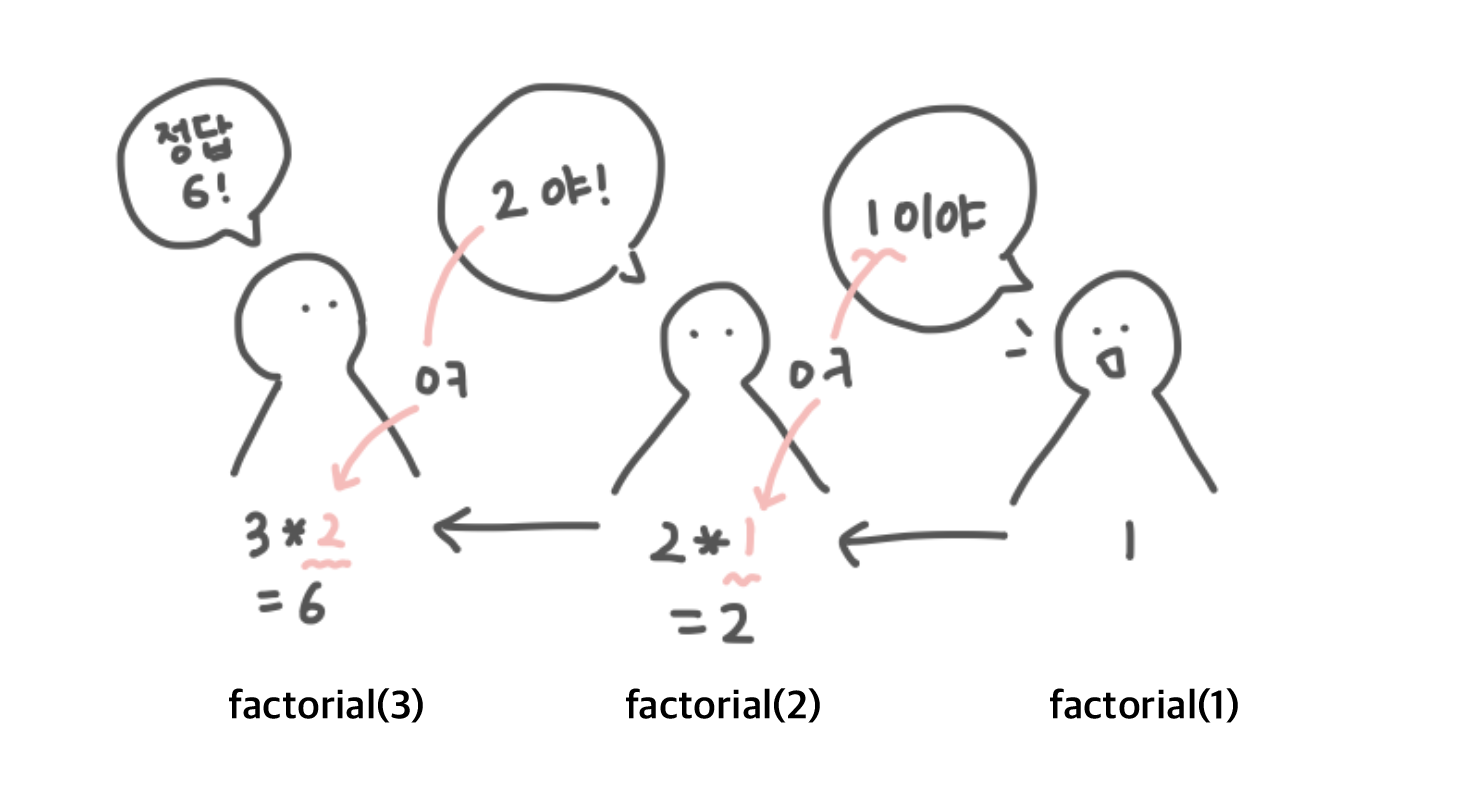
그 밑에 있는 그림은 스택에 쌓여있는 함수들을 사람으로 표현해본 그림이다. 호출 당한 함수가 호출한 함수에게 자신의 결과값을 알려주고, 그 값을 전달 받은 함수는 자기가 원래 갖고있던 값과 곱셈 연산을 해서 다시 다른함수에게 전달하는 모습을 볼 수 있다.
꼬리 재귀 방식
그럼 이제 꼬리 재귀 방식을 사용해서 팩토리얼 연산을 한번 해보자. 앞서 꼬리 재귀는 '재귀 호출이 끝나면 아무 일도 하지 않고 결과만 바로 반환되도록 하는' 방법이라고 언급했다. 코드의 마지막 부분을 보면, 일반적인 재귀에서는 n * factorial(n-1) 를 반환했던 것과는 달리 곱하기 같은 연산 없이 factorial(n - 1, n * total)이라는 값만 반환하는 것을 볼 수 있다. 꼬리 재귀 방식에서는 total이라는 이미 곱셈 연산을 마친 값을 매개변수로 두었기 때문이다.
function factorial(n, total = 1){
if(n === 1){
return total;
}
return factorial(n - 1, n * total);
}
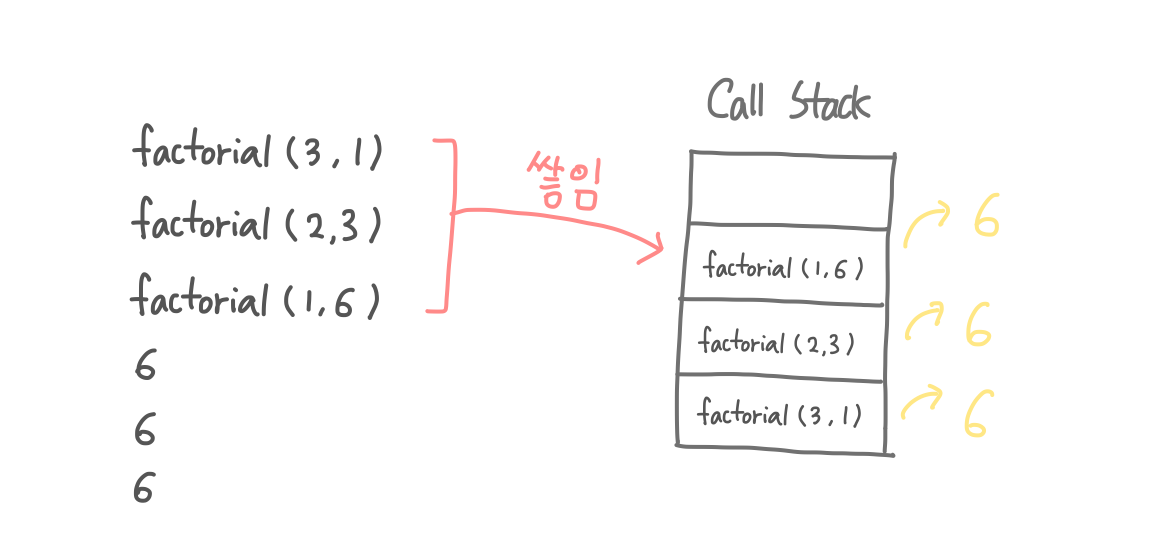
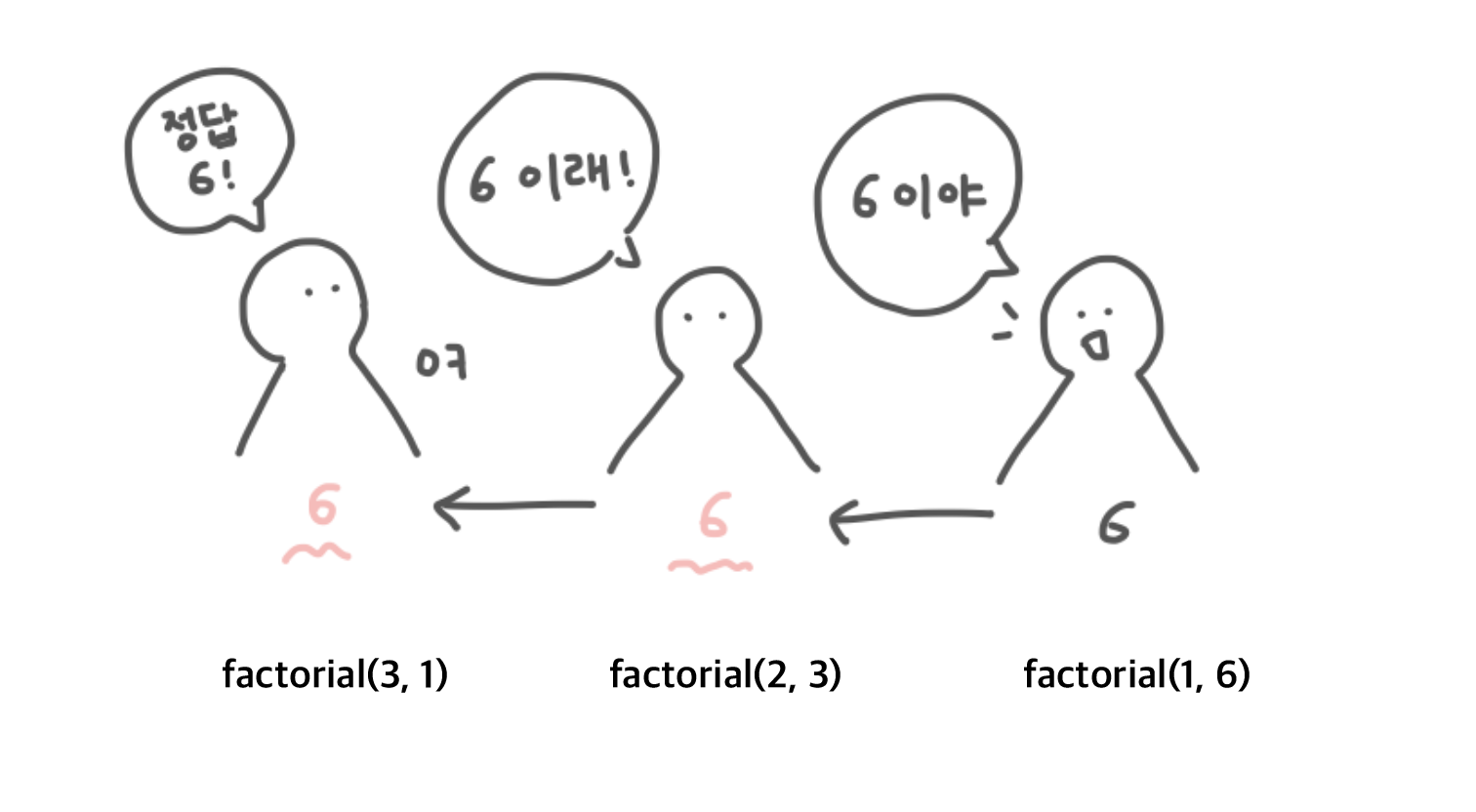
위의 코드를 실행시켜보면 스택에는 아래처럼 함수들이 쌓이게 된다. 언뜻보면 비슷해보일 수 있지만 가장 큰 차이는 값들을 반환할 때 나타난다. 그림을 보면 가장 마지막으로 계산된 total 값인 6이 그대로 전달되는 걸 볼 수 있다. 각 함수들은 별도의 연산 없이, 정말 아무것도 안하고 이 값을 전달만 하는 것이다. 위에서 봤던 일반 재귀는 값을 받으면, 그 값에 연산을 하고 다른 함수에게 전달을 해줬었다. 하지만 꼬리재귀는 '아무것도 하지 않고' 값을 전달한다.
다시 한 번 정리해보자. 일반 재귀의 마지막 부분은 아래처럼 생겼었다. factorial(n-1)이 바로 호출당한 함수인데, 이 함수는 스택에 쌓였다가 빠져 나올 때 원래 자기 자리로 돌아가서 앞쪽의 n과 곱해져야 한다. 다시말해 '자기 자리'를 기억하고 있어야 한다는 뜻이다. 위에서 재귀에 대해 설명할 때 스택에 입력값(매개변수), 결과값(리턴값), 그리고 리턴 후 돌아갈 위치 등이 저장된다고 언급했는데, 이 중 리턴 후 돌아갈 위치값이 바로 여기서 말하는 '자기 자리'이다.
return n * factorial(n-1);
하지만 꼬리 재귀의 마지막 부분을 보면 따로 하는 일(연산 등..)이 없기 때문에 굳이 자기 자리를 기억하지 않아도 된다. 그래서 스택에 리턴 후 돌아갈 위치값을 저장할 필요도 없어진다.
return factorial(n - 1, n * total);
마지막으로 정리하면 꼬리 재귀는 자신이 호출한 함수한테 받은 결과값에 아무 일도 하지 않고 바로 반환 하기 위해 꼬리(마지막 부분)에서 함수를 호출하는 방식이라고 할 수 있다! 🦎
'Base > 알고리즘' 카테고리의 다른 글
| 퀵 정렬(Quick Sort) (0) | 2021.06.01 |
|---|---|
| DFS(깊이우선탐색) / BFS(너비우선탐색) (0) | 2021.01.24 |
| 선형 검색, 이진 검색 (단순 검색 알고리즘) (0) | 2021.01.09 |
| 빅오(Big-O) 표기법 (0) | 2021.01.09 |




댓글