Tree (트리)
트리는 노드(node)들을 선(edge)으로 연결한 계층형 자료구조이다. 제일 위에 root(뿌리) 노드 하나가 있고, 그 아래 나머지 자식 노드들이 선으로 연결되고 또 연결되는 구조이다. 나무를 거꾸로 한 모양같다고 해서 트리라는 이름이 붙여졌다고 한다.

관련 용어
루트노드(root node) : 최상위 노드
리프노드(leaf node) : 자식이 없는 노드
부모 노드(parent node) : 노드에 연결된 한단계 상위 레벨 노드
자식노드(child node) : 서브트리의 루트노드들 ex. A의 자식 : B, C
형제노드(sibling) : 같은 부모 + 같은 depth에 있는 노드들
노드의 차수 : 한 노드의 서브트리의 수
트리의 차수 : 트리노드 차수들 중 최대 차수
트리의 높이(height) : 트리 중 가장 긴 경로의 간선 개수
트리의 깊이(depth) : 루트에서 현재 노드 사이의 간선 개수
트리의 레벨(level) : 트리의 층수 ( depth+1 )
이진 트리 (Binary Tree)
이진트리(binary tree)는 노드가 왼쪽 자식, 오른쪽 자식을 갖는 트리이다. 각 노드의 2명 이하의 자식만 가질 수 있다.
이진 트리 종류
이진 트리는 자료를 삽입하거나 삭제하는 방법에 따라 정 이진 트리, 완전 이진 트리, 포화 이진 트리로 나뉜다.
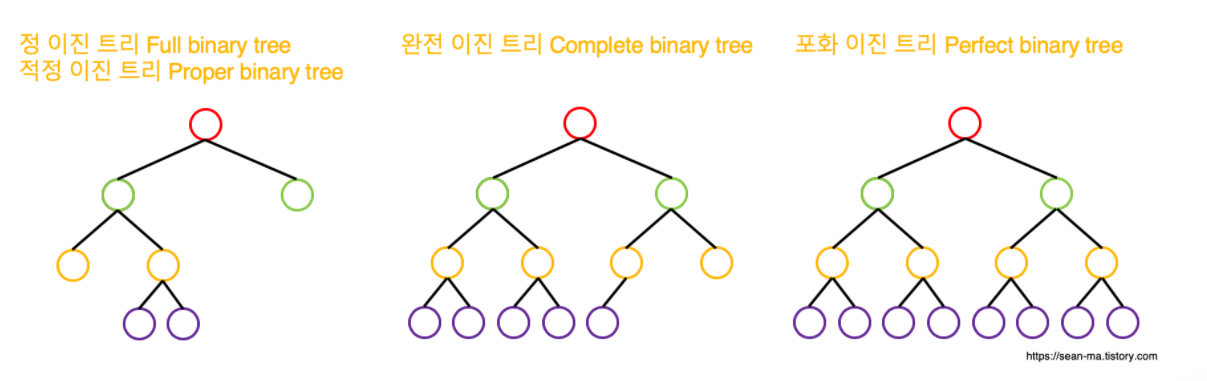
1. 정 이진 트리 (Full binary tree)
정 이진 트리는 각 노드가 자식 노드를 2개씩 갖는 순서가 있는 트리를 말한다. 따라서 자식 노드 개수는 홀수 개일 수 없다.
2. 완전 이진 트리 Complete binary tree)
완전 이진 트리의 경우 루트부터 노드가 채워져 있고, 같은 레벨이면 왼쪽에서 오른쪽으로 노드가 채워진다. (부모 - 왼쪽자식 - 오른쪽자식 순) 이렇게 마지막 레벨을 제외하고는 모든 노드가 빈틈없이 채워진 형태이다.
3. 포화 이진 트리 (Perfect binary tree)
포화 이진 트리는 모든 레벨이 가득 찬 이진 트리를 말한다.
Binary Search Tree (이진 탐색 트리)
앞서 살펴봤던 이진트리(Binary Tree)는 노드가 최대 2명의 자식을 가지는 트리를 의미했다. 비슷한 이름의 이진탐색트리(Binary Search Tree, BST)는 이진트리에 두 가지 조건이 추가된다. 1) 왼쪽자식은 루트노드보다 작을 것, 2) 오른쪽 자식은 루트노드보다 클 것 바로 이 두 가지이다. 이진 탐색 트리에서는 노드의 값이 어떤 기준으로 정렬되느냐에 따라 순서가 존재하게 된다.
트리 순회 (Tree Traversal)
트리 순회는 트리에 있는 노드들을 하나도 빠뜨리지 않고, 중복없이 딱 한번씩만 방문하는 체계적인 방법을 말한다. 노드를 어떤 순서로 방문하는 지에 따라 전위순회(preorder), 중위순회(inorder), 후위순회(postorder)로 구분된다.
1. 전위 순회(Preorder Traversal)
부모 → 왼쪽자식 → 오른쪽 자식 순서로 방문
2. 중위 순회(Inorder Traversal)
왼쪽자식 → 부모 노드 → 오른쪽 자식 순서로 방문
3. 후위 순회(Postorder Traversal)
왼쪽 자식 → 오른쪽 자식 → 부모 순서로 방문
그래프(Graph) vs 트리(Tree)
| 그래프(Graph) | 트리(Tree) | |
| 정의 | 노드간 관계를 간선으로 연결한 자료구조 (네트워크 모델) |
노드들을 간선으로 연결한 계층형 자료구조 (계층 모델) |
| 방향성 | 방향그래프, 무방향그래프 | 방향그래프 |
| 루트노드 | 루트노드 X | 루트노드 1개 존재 O |
| 부모-자식 | 부모-자식관계 존재 X | 부모-자식관계 존재 O |
| 경로 | - | 두 노드 사이에 유일한 경로 존재 |
'Base > 자료구조' 카테고리의 다른 글
| Data Structure(4) Graph(그래프) (0) | 2021.01.22 |
|---|---|
| Data Structure(3) Hash Table(해시 테이블) (0) | 2021.01.21 |
| Data Structure(2) Linked List (연결 리스트) (0) | 2021.01.21 |
| Data Structure(1) Stack (스택), Queue (큐) (0) | 2021.01.19 |




댓글